By Theron Wierenga View In Digital Edition
Last time's article finished with the chessboard circuit and its construction. Also presented was how the software knows a piece has been moved and what piece it was. Let's move on to the software needed to take two players through a game of chess.
A flowchart of the Teensy 3.1 loop() function is shown in Figure 1.
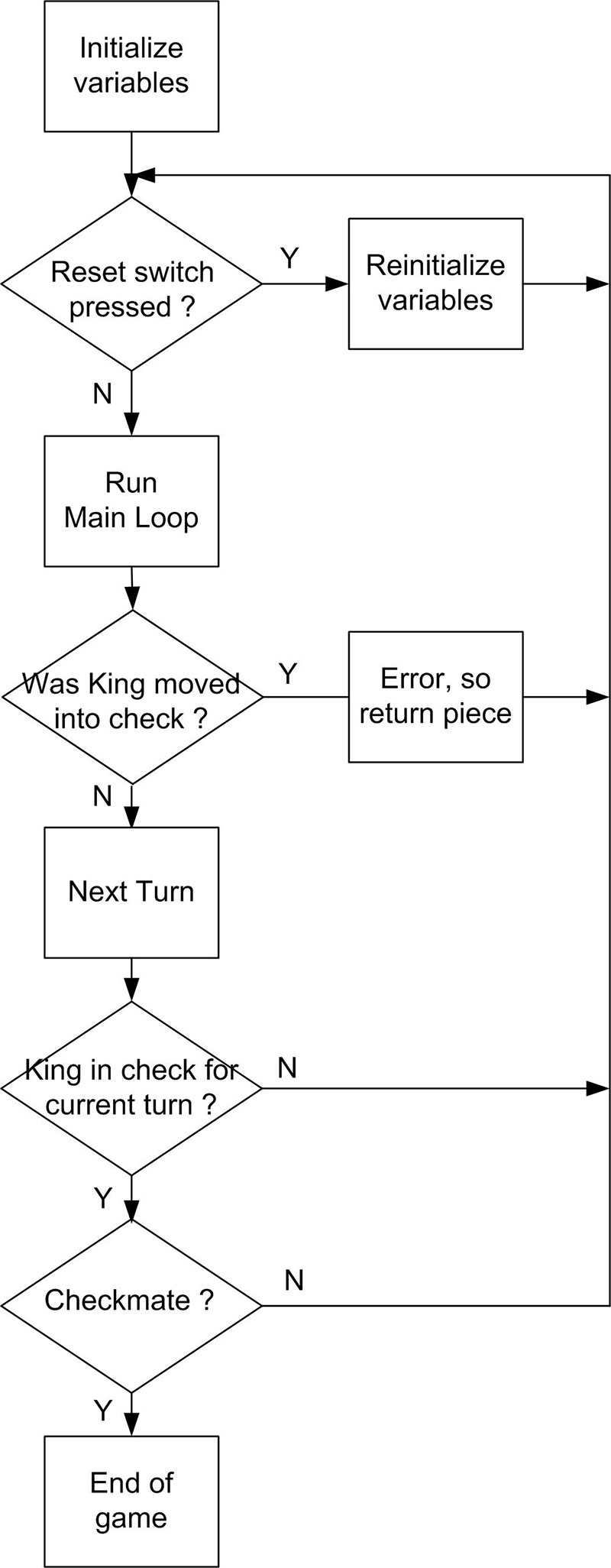
FIGURE 1. Flowchart of the Teensy 3.1 loop().
The mainLoop() function contains the majority of the functionality of the chessboard program; a simplified flowchart of it appears in Figure 2.
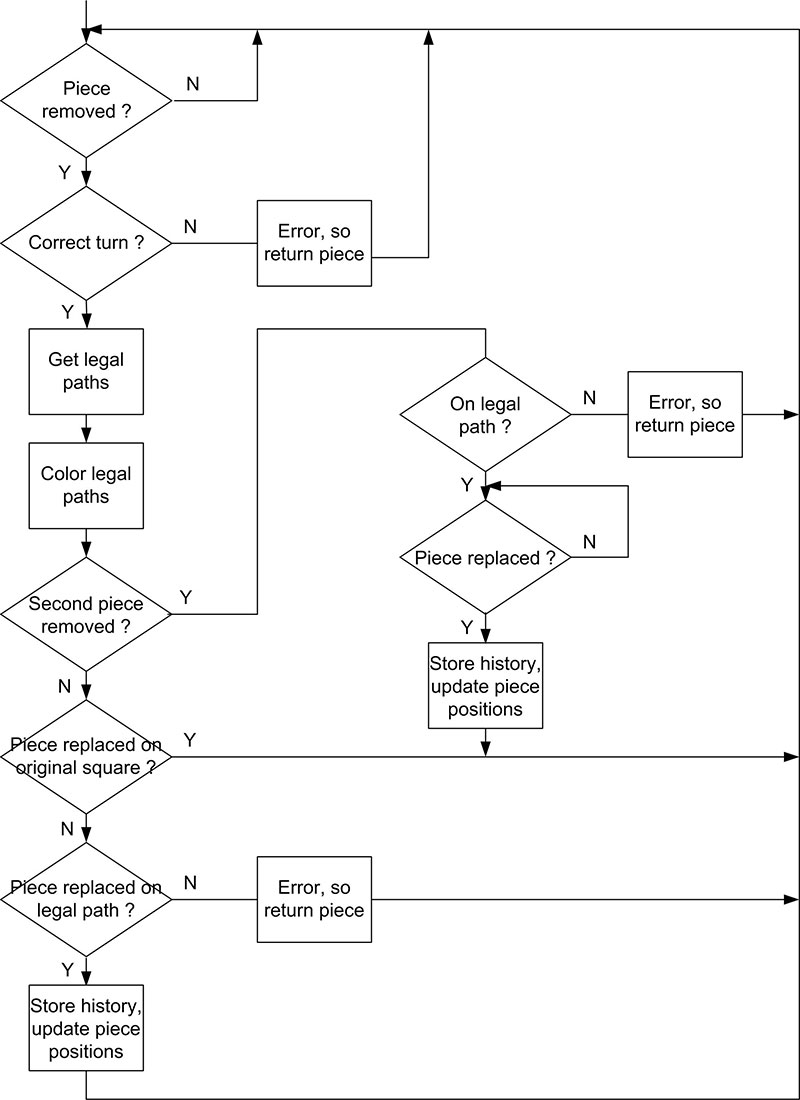
FIGURE 2. Flowchart of the mainLoop() function.
The mainLoop() function processes three possible legal moves for each turn:
The mainLoop() function starts by simply looking for a piece that has been removed from the board. Here is a code fragment:
int total1 = 0, total2 = 0, total3 = 0; // For different reads of total number of pieces on the board
do
{
total1 = readHall(piecesTemp1); // Read the Hall Effect sensors
}while (total1 == bdCount); // Wait for a change
The readHall() function returns the total number of pieces found on the board, which is compared to the current board count bdCount. Next, the temporary array pieceTemp1 is compared with piecesCurrent which holds the current piece array. The comparePieceArrays() function does this. It simply loops through all 64 board positions until it finds the square that doesn’t match and then writes this into xx and yy, which are variables passed by reference. Whatever variable passed to xx and yy will now have the position in the array of the piece that was removed.
This function is a good example of the code not being efficient, but instead being easy to understand. It wades through possibly all 64 board squares to find the changed piece. In return for this, the code structure is easy to comprehend — a loop looking for non-matching numbers:
// Compare piece arrays
bool comparePieceArrays(int &xx, int &yy, byte piecesCurrent[][8], byte piecesTemp1[][8])
{
for (int y = 0; y < 8; y++)
{
for (int x = 0; x < 8; x++)
{
if (piecesTemp1[y][x] != piecesCurrent[y][x])
{
// First piece that doesn't match previous,
// Write to xx, yy and return
xx = x; yy = y;
return false; // arrays are different
}
}
}
return true; // arrays are the same
}
After some error checking (such as this square containing a piece of the correct turn, i.e., color), the next thing needed is to find the path (the list of squares) that this piece can move to legally. This list consists of three arrays — pathX[ ], pathY[ ], pathVal[ ] — and pathCount; the latter keeping track of how many squares are stored in the arrays.
The function that stores the squares — getPaths() — is very lengthy as it needs to be able to find the different legal paths for all the different pieces.
The chess pieces group themselves into two distinct methods to obtain the paths. The bishop, rook, and queen can all slide across the board in straight lines: either perpendicular as the rook, diagonally as the bishop, or both as the queen. So, for example, the queen’s paths are found by:
// Queen ******************************************************************************* Queen Queen Queen
if ((val == BLACK_QUEEN) || (val == WHITE_QUEEN))
{
// x and y are the starting positions
getSinglePathinPaths(x + 2, y + 2, 1, 1, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2,-1,-1, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2, 1,-1, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2,-1, 1, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2, 1, 0, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2,-1, 0, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2, 0, 1, pathCount, turn);
getSinglePathinPaths(x + 2, y + 2, 0,-1, pathCount, turn);
}
The function getSinglePathinPaths() is called eight times; once for each direction it can move. Note that the third and fourth parameters of this function are either 0, 1, or -1. These values are added to the queen’s x and y position in a loop, depending on the perpendicular or diagonal direction in which the piece can move.
When the loop hits a square that is not empty, it checks to see if the piece there is an opponent’s and if so, stores it in the path as well, and then returns from the function. If it wasn’t an opponent, it was either one of its own pieces or off the board.
Note that the count variable is passed by reference, so that it keeps an ongoing total of the number of squares stored in the arrays when the getSinglePathinPaths() function is called multiple times.
The code for the bishop’s and rook’s paths contain only four calls to getSinglePathinPaths() for the various directions they can move:
// Follow a single path to its end
void getSinglePathinPaths(int xx, int yy, int xdir, int ydir, int &count, int turn)
{
// This function starts with the xx, yy position of a square and xdir and ydir directions to add
// to the square's position with every loop. The loop continues as long as the squares are EMPTY.
// When it hits a square occupied it checks to be sure it is an opponent's piece and then will
// add this to the path.
xx = xx + xdir;
yy = yy + ydir;
while (piecesValCur[yy][xx] == EMPTY)
{
pathY[count] = yy - 2; pathX[count] = xx - 2; pathVal[count] = piecesValCur[yy][xx];
count++;
xx = xx + xdir;
yy = yy + ydir;
}
if (((turn == WHITE) && (piecesValCur[yy][xx] >= BLACK_PAWN) && (piecesValCur[yy][xx] <= BLACK_KING)) ||
((turn == BLACK) && (piecesValCur[yy][xx] >= WHITE_PAWN) && (piecesValCur[yy][xx] <= WHITE_KING)))
{
pathY[count] = yy - 2; pathX[count] = xx - 2; pathVal[count] = piecesValCur[yy][xx]; count++;
}
}
Finding the paths for the knight is a different matter since it can jump to a possible eight different positions. A brute force method is used here, and a similar technique is used for the king. The pawn uses more complex code because of its different movements.
The eight relative moves of the knight are stored in the i[ ] and j[ ] arrays, which are then just added to the starting position in a loop. If the square has an opponent’s piece in it or if it is empty, the square is stored in the path array:
// Knight *************************************************************************** Knight Knight Knight
if ((val == BLACK_KNIGHT) || (val == WHITE_KNIGHT))
{
// x and y are the starting positions
int i[8] = {1, 2, -1, -2, -1, -2, 1, 2};
int j[8] = {2, 1, -2, -1, 2, 1,-2,-1};
// Check all eight possible moves
for (int k = 0; k < 8; k++)
{
xx = x + 2 + i[k]; yy = y + 2 + j[k];
if (((turn == WHITE) && (piecesValCur[yy][xx]>=BLACK_PAWN) && (piecesValCur[yy][xx]<=BLACK_KING)) ||
((turn == BLACK) && (piecesValCur[yy][xx]>=WHITE_PAWN) && (piecesValCur[yy][xx]<=WHITE_KING)) ||
(piecesValCur[yy][xx] == EMPTY))
{
pathY[pathCount] = yy - 2; pathX[pathCount] = xx - 2; pathVal[pathCount] = piecesValCur[yy][xx];
pathCount++;
}
}
}
Details for all the pieces can be found in the complete program (available in the downloads). After the path for a piece is stored, it is displayed on the chessboard. I chose green to color the squares that are empty and yellow for a square that has an opponent’s piece that can be captured. The Boolean true in the colorSquare() function’s parameter list will turn on each square’s color as it proceeds through the loop of squares to count in the path:
// Color the positions a piece can legally move to
void colorPath(int count, int turn)
{
for (int i = 0; i < count; i++)
{
if (pathVal[i] == EMPTY)
colorSquare(pathX[i], pathY[i], colors[GREEN], true);
if ((turn == WHITE) && (pathVal[i] >= BLACK_PAWN) && (pathVal[i] <= BLACK_KING))
colorSquare(pathX[i], pathY[i], colors[YELLOW], true);
if ((turn == BLACK) && (pathVal[i] >= WHITE_PAWN) && (pathVal[i] <= WHITE_KING))
colorSquare(pathX[i], pathY[i], colors[YELLOW], true);
}
}
The function to determine if a king is in check is a little more difficult conceptually. It's necessary to look at the paths for pieces in the next turn. So, if it is the WHITE turn, then it looks at the paths for all the BLACK pieces to see if the WHITE king is in the path of a BLACK piece. If the program finds the king in check, it colors the square of the king and the piece placing the king in check violet. Figure 3 is a simplified flowchart followed by the complete kingInCheck() function
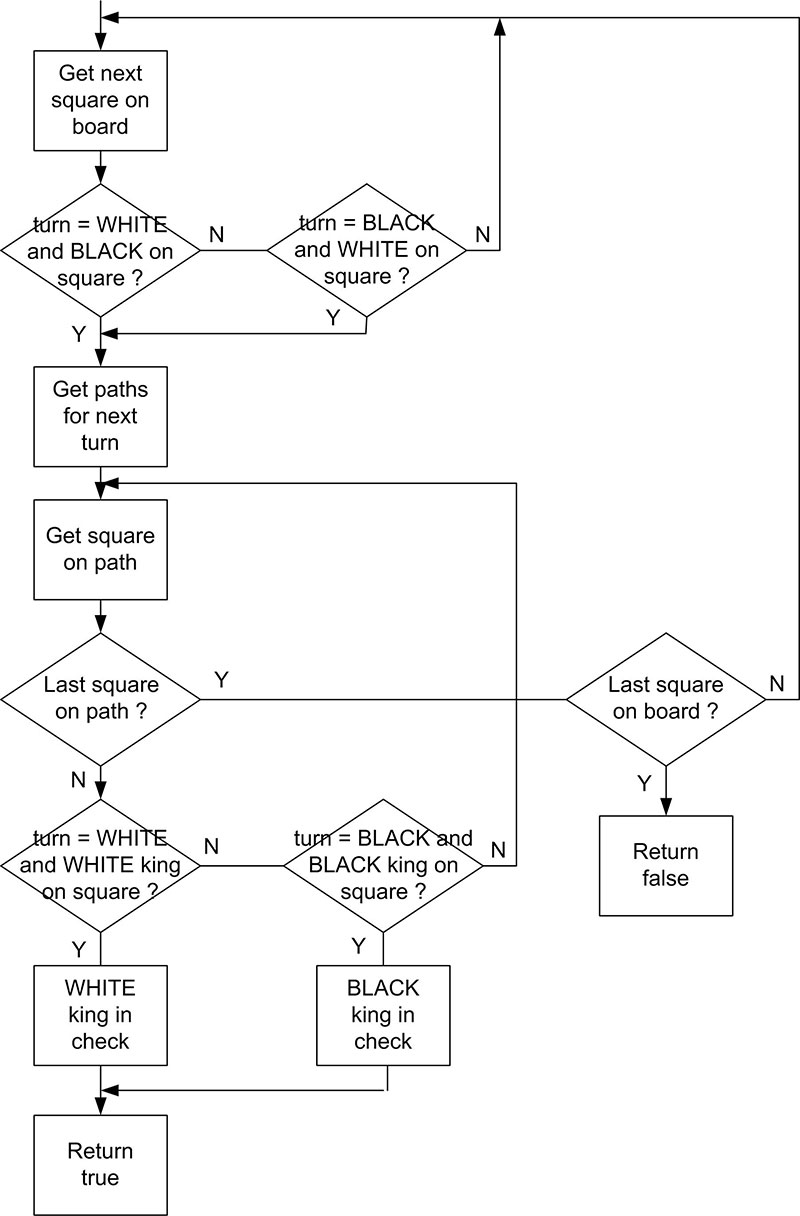
FIGURE 3. Determining if the king is in check flowchart.
// Is the King in check ?
bool kingInCheck(int turn)
{
// This one is tricky, we go though entire array looking for the next turn's pieces
// Then we find the paths for the next turn's pieces and if the turn's king
// is on one of these paths then that king will be in check. We color the square
// with the piece that puts the king in check violet.
pathCount = 0;
for (int y = 0; y < 8; y++)
{
for (int x = 0; x < 8; x++)
{
if (((turn==WHITE)&&(piecesValCur[y+2][x+2]>=BLACK_PAWN)&&(piecesValCur[y+2][x+2]<=BLACK_KING)) ||
((turn==BLACK)&&(piecesValCur[y+2][x+2]>=WHITE_PAWN)&&(piecesValCur[y+2][x+2]<=WHITE_KING)))
{
getPaths(piecesValCur[y + 2][x + 2], x, y, nextTurn(turn));
for (int i = 0; i < pathCount; i++)
{
if (((pathVal[i]==BLACK_KING)&&(turn==BLACK))||((pathVal[i]==WHITE_KING)&&(turn==WHITE)))
{
lcd.setCursor(0, 4);
if (turn == BLACK)
{
lcd.print("Black King in Check");
}
else
{
lcd.print("White King in Check");
}
// Save the position of the king in check
xKingCheck = pathX[i]; yKingCheck = pathY[i];
// Save the position of the attacking piece
xAttackPos = x; yAttackPos = y;
pathToKingInCheck(xKingCheck, yKingCheck, xAttackPos, yAttackPos);
colorSquare(xAttackPos, yAttackPos, colors[VIOLET], true);
colorSquare(xKingCheck, yKingCheck, colors[VIOLET], true);
pathCount = 0;
return true;
}
}
pathCount = 0;
}
}
}
return false;
}
The checkMate() function was the most challenging portion of the software to write. In order to achieve checkmate and win the game, the king must be placed in check, and on the next move the king must not be able to get out of check. Looking at the reverse, in order to not be in checkmate after the king has been placed in check, the king must:
Figure 4 is a simplified flowchart of checkMate() which is followed by the function code.
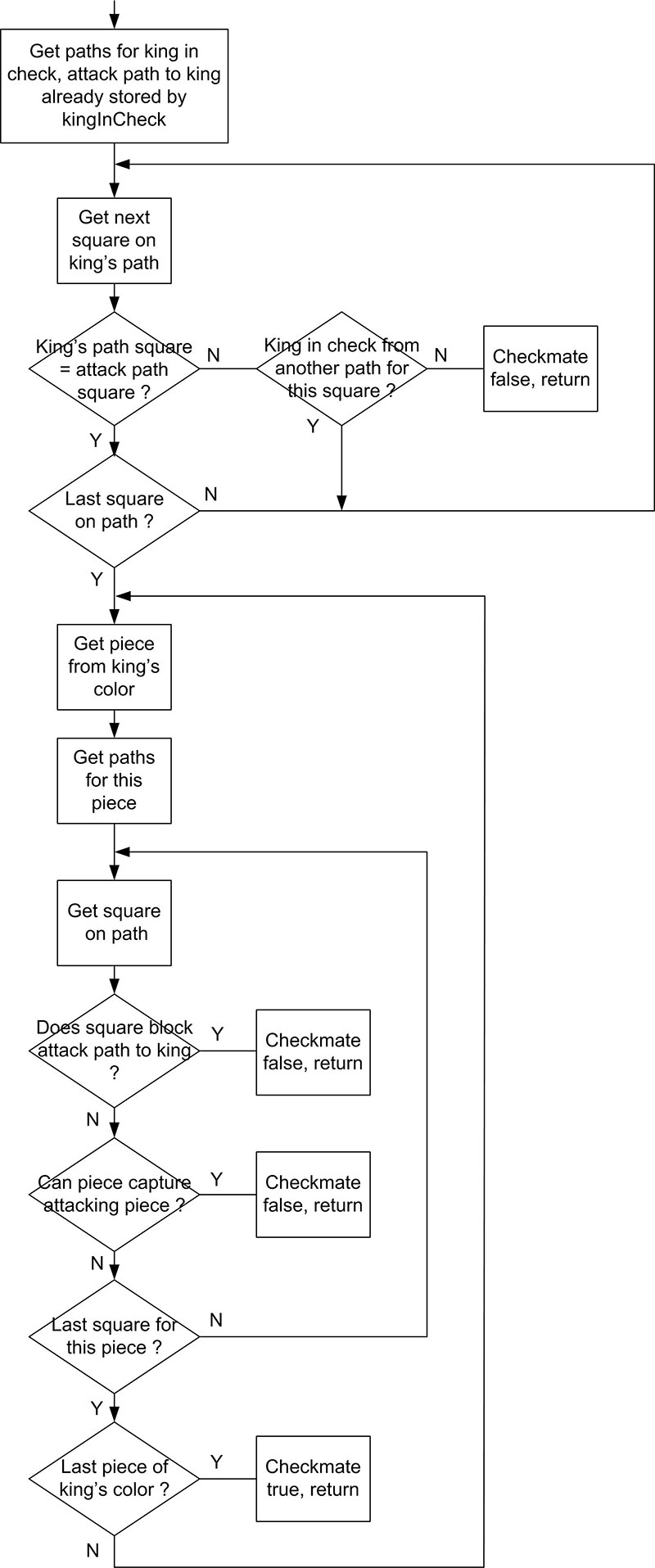
FIGURE 4. Flowchart of checkMate() function.
// Are we in checkmate ? return true if in checkmate
bool checkMate(int turn)
{
// Function kingInCheck has stored king position in xKingCheck, yKingCheck, and also stored
// xAttackPos and yAttackPos of attacking piece.
// pathToKingInCheck(xKingCheck, yKingCheck, xAttackPos, yAttackPos) stores the path between
// the two in int variables xPathtoKing[6], yPathtoKing[6], and pathtoKingCount
// can the king move to get out of check
// get the paths for the king which is in check
getPaths(piecesValCur[yKingCheck + 2][xKingCheck + 2], xKingCheck, yKingCheck, turn);
printPaths(xKingCheck, yKingCheck);
// pathtoKingCount needs to be zeroed before returning this function
for (int i = 0; i < pathCount; i++) // paths king can move to
{
for (int j = 0; j < pathtoKingCount; j++) // attack path to king
{
if (!((pathX[i] == xPathtoKing[j]) && (pathY[i] == yPathtoKing[j])))
{
// There is a square the king can move to that is not on the path
// from the attacking piece to the king, but will king move into check from another piece?
myDebug(pathX[i], pathY[i], "Path king can move to");
if (squareInOpponentPath(pathX[i], pathY[i], turn))
{
// this square will have king in check if king moves there
continue;
}
else
{
// square is open - no checkmate
pathtoKingCount = 0;
pathCount = 0;
return false;
}
}
}
}
// now we check to see if we can move a piece to block attacking piece
for (int y = 0; y < 8; y++)
{
for (int x = 0; x < 8; x++)
{
if (((turn == BLACK) && (piecesValCur[y + 2][x + 2] >= BLACK_PAWN) && (piecesValCur[y + 2][x + 2] <= BLACK_QUEEN)) ||
((turn == WHITE) && (piecesValCur[y + 2][x + 2] >= WHITE_PAWN) && (piecesValCur[y + 2][x + 2] <= WHITE_QUEEN)))
{
pathCount = 0;
getPaths(piecesValCur[y + 2][x + 2], x, y, turn);
// printPaths(x, y);
for (int i = 0; i < pathCount; i++)
{
for (int j = 0; j < pathtoKingCount; j++)
{
if (((pathX[i] == xPathtoKing[j]) && (pathY[i] == yPathtoKing[j])) || // piece can move to attacking path
((pathX[i] == xAttackPos) && (pathY[i] == yAttackPos))) // or can capture the attacking piece
{
// we can block attacking piece
myDebug(pathX[i], pathY[i], "Blocking piece for king");
pathtoKingCount = 0;
pathCount = 0;
return false;
}
}
}
}
}
}
pathtoKingCount = 0;
// if we get here, checkmate
lcd.setCursor(0, 4);
lcd.print(" CHECKMATE! ");
return true;
}
Future Enhancements
Throughout the Teensy 3.1 chess program, there are many lines that print to the serial monitor of the Arduino GUI with the USB cord in place. These could be eliminated from the program or commented out, but have been left in place as they were helpful when debugging, and will be informative to a user in understanding how the program is operating.
A number of functions were also written that simply print information to the serial monitor for debugging, such as printPaths(), printPiecesLoc(), printPiecesVal(), and myDebug(). If you want to modify this program, you should find these functions useful.
A possible enhancement to the existing code might be suggesting moves to each player. Changing the program to have the computer play against a person would require a major effort. The computer used for this could be the Teensy 3.1, or a PC could be interfaced to the chessboard. Surprisingly, the Teensy 3.1 only uses 12% of its program space and 10% of its dynamic memory for the software presented here, so there is lots of room for additional code.
This project has given me a lot of satisfaction, and is one of those where adding possible additions to the code will be a challenging and interesting activity.
It’s your move now. NV
It should be pointed out that if you intentionally try to fool the chessboard by doing something far outside the rules of chess — like picking up multiple pieces and switching them — it's not too hard to confuse the program or even lock it up. The software will do a good bit of checking to look for reasonable errors, but it cannot identify every trick you try. This should not present a problem if you simply stick to the rules of chess. This would not be the case if each piece could identify itself uniquely.
For this, it would be necessary to have something like an RFID tag on each chess piece and an RFID reader that could scan all 64 positions. A barcode reader might be another approach to this. The difficulty here is building a 64-position reader that will only detect and identify the piece above it.
When a piece is captured, the user should first remove the capturing piece, then remove the captured piece and then replace the capturing piece on the captured piece's square. If you use the capturing piece to slide or knock over the captured piece, you will most likely get an error which may not be recoverable, as the magnets can trigger other Hall-effect sensors.
If you try to take two turns in a row or place a piece on a square which is not allowed, or make a move that places your king in check, all the LEDs on the board will turn red, indicating an illegal move. When you return the offending piece to its original position, the board will revert to blue and red squares and play can continue.
